Taylor展開

ある関数$f$の点$x_0$の周りでのTaylor展開は以下のように書ける：

\[\begin{aligned} f(x) &= f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)(x-x_0)^2}{2!} + \cdots. \\ &= \sum^{\infty}_{k=0}f^{(k)}(x_0)\frac{(x-x_0)^k}{k!}. \end{aligned}\]

例えば，正弦関数を展開すると，

\[\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots + (-1)^n\frac{x^{2n+1}}{2n+1}.\]

数値的手法においては，Taylor展開における最初のいくつかの項だけを用いて関数を近似することが頻繁に行われる．次に，いくつの項を使えば元の関数を十分近似できるのかということに興味が出る．

Big $O$記法とBig $O_p$記法

定義 1. （Big $O$記法）二つの数列${a_n}$と${b_n}$について，$n\to\infty$で$|a_n/b_n|$が有界であるとき$a_n=O(b_n)$と表す．

$O$記法は，興味のある数列${a_n}$の比較対象${b_n}$に対する相対的なサイズを測っているとみなせる．例えば二つの$N\times N$正方行列の和を計算するには$N^2$の操作が必要になるので，この操作は$O(N^2)$であると言える．また，行列積の操作は$O(N^3)$であると言える．

正弦関数の例で，例えば$s_2(x)$を$\sin(x)$のTaylor展開の最初の2つの項の和

\[s_2(x) = x - \frac{x^3}{3!}\]

と定義し，$s_2(x)$によって$\sin(x)$を近似することを考える．このときの誤差は

\[e(x) = \sin(x) - s_2(x) = \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\]

と書くことができ，$x\to 0$で$e(x)/x^5$は有界であるので，$s_2(x)$の近似誤差は$O(x^5)$であると評価できる．

一般的な慣習として，

定数は無視する．つまり，$O(2N)$，$O(5N)$などとは書かずに$O(N)$と書く．
同じオーダーはまとめることができる．つまり，$O(N) + O(N) = 2O(N) = O(N)$．
大小の2つのオーダーは大きい方にまとめることができる．例えば，$O(N) + O(N^{1/2})=O(N)$．

確率的な状況において$O()$記法を利用するために，以下のような定義の修正が考えられる．

定義 2. （$O_p(1)$） $X_N$を確率変数列とする．ある$\epsilon>0$について，$N(\epsilon)$と$\delta>0$が存在して，$N>N(\epsilon)$で $P\Big(|X_n|\leq\epsilon\Big)\geq 1-\delta$ を満たすとき，$X_n=O_p(1)$であるとする．このとき$X_N$は確率有界であるという．

定義 3. （Big $O_p$記法） $X_n/b_n$が$O_p(1)$のとき，$X_n$は$O_p(b_n)$であるとする．

統計学において特に興味の対象となる例として，平均$\mu$，分散$\sigma^2$の分布からの標本平均$\bar{X}_N$と$\mu$との誤差$\epsilon_N = \bar{X}_N - \mu$がある．中心極限定理から，

\[\frac{\bar{X}_N - \mu}{\sigma/\sqrt{N}}\sim N(0, 1)\]

であり，左辺が確率有界であるので，

\[\frac{\bar{X}_N - \mu}{\sigma/\sqrt{N}} = O_p(1)\]

となることがわかる．$\sigma$が$N$に関係のない量であることに注意すると，ここから直ちに，

\[\bar{X}_N - \mu = O_p(\sigma/\sqrt{N}) = O_p(n^{-1/2})\]

となる．

特性関数

確率分布の特定のための有用なツールとしては積率母関数があるが，積率母関数は常に存在することは保証されないという欠点がある．それに対して，以下で定義される，積率母関数の複素拡張である特性関数は常に存在し，積率母関数と多くの性質を共有することが知られている．

\[\phi_X(t) = \mathbb{E}[e^{itX}].\]

また，もし関数列$\phi_{X_N}(t)$が$\phi_X(t)$に収束するとき，$X_N$は$X$に分布収束するという．

キュムラント

積率母関数の対数の微分を$x=0$で評価することで得られるキュムラントは，確率変数の和の分布について考える際に非常に有用なツールである．

$X$を特性関数

\[\phi_X(t) = \mathbb{E}[e^{itX}] = \int e^{itx}f(x)dx\]

をもつ確率変数とすると，特性関数は以下のように展開できる．

\[\phi_X(t) = \exp\Big\{\sum_{n=1}\frac{\kappa_n(it)^n}{n!}\Big\}\]

ここで$\kappa_j$は$j$番目のキュムラント．また，$\phi_X$の対数を取ると，

\[K(t) = \sum^\infty_{n=0}\frac{\kappa_n(it)^n}{n!}\]

と，キュムラント母関数が得られる．

例えば，$X\sim N(0,1)$とすると，

\[\begin{aligned} \phi(t) = \mathbb{E}[e^{itX}] &= \int^\infty_{-\infty}e^{itx}\frac{e^{-x^2/2}}{\sqrt{2\pi}} \\ &= \int^\infty_{-\infty}\frac{\exp{\{itx - x^2/2 + t^2/2 - t^2/2\}}}{\sqrt{2\pi}}dx \\ &= e^{-t^2/2}\int^\infty_{-\infty}\frac{\exp{\{t^2/2+itx-x^2/2\}}}{\sqrt{2\pi}}dx \\ &= e^{-t^2/2}\int^\infty_{-\infty}\frac{\exp{\{t+ix}^2/2\}}{\sqrt{2\pi}}dx \\ &= e^{-t^2/2}. \end{aligned}\]

また，キュムラント母関数は

\[K(t) = \log{\phi(t)} = -\frac{t^2}{2}.\]

キュムラントの性質

独立な確率変数$X$と$Y$の和$S=X+Y$を考える．このとき，$\phi_S(t) = \phi_X(t)\phi_Y(t)$かつ$K_S(t) = K_X(t) + K_Y(t)$であることが直ちにわかる．

次に，確率変数の定数倍$cX$を考えると，

\[\phi_{cX}(t) = \phi_X(ct) \Rightarrow K_{cX}(t) = K_X(ct) \Rightarrow \kappa_j(cX) = c^j\kappa_j(X).\]

上記の二つの性質を使うことで，$N$個のi.i.dな確率変数の和と平均についてのキュムラントを考えることができる． $S=\sum^N_{i=1}X_i$，$\bar{X} = S/N$とすると，キュムラントはそれぞれ

\[\begin{aligned} \kappa_i(S) &= \sum\kappa_i(X) = N\kappa_i(X) \\ \kappa_i(\bar{X}) &= \frac{\kappa_i(X)}{N^{i-1}}. \end{aligned}\]

次に，以下のような特性関数の展開を考える：

\[\begin{aligned} \phi_X(t) = \mathbb{E}[e^{itX}] &= \int e^{itx}f(x)dx \\ &= \int\Big\{1 + itx + \frac{(itx)^2}{2!} + \frac{(itx)^3}{3!}+\cdots \Big\}f(x)dx \\ &= \int\Big\{f(x) + itxf(x) + \frac{(it)^2x^2f(x)}{2!} + \frac{(it)^3x^3f(x)}{3!}+\cdots \Big\}dx \\ &= 1 + it\mathbb{E}[X] + \frac{(it)^2\mathbb{E}[X^2]}{2!} + \frac{(it)^3\mathbb{E}[X^3]}{3!} + \cdots. \end{aligned}\]

Edgeworth展開

定理 4. （反転定理） $Y$を特性関数$\phi_Y(t)$および累積分布関数$F_Y(y)$をもつ確率変数とする．このとき以下が成り立つ．

\[f_Y(y) = \frac{1}{2\pi}\int^\infty_{-\infty}e^{-ity}\phi_Y(t)dt.\]

反転定理は密度関数を特性関数によって記述することができる点で，有用な場面が多くある．

$\phi(x)$を標準正規分布の密度関数とすると，$r^{th}$ Hermite多項式$H_r(x)$を以下のように定義する．

\[H_r(x) = \frac{(-1)^r}{\phi(x)}\frac{d^{(r)}\phi(x)}{(dx)^r}.\]

特に重要な値は， $\begin{aligned} H_1(x) &= x \\ H_2(x) &= x^2 - 1 \\ H_3(x) &= x^3 - 3x \\ H_4(x) &= x^4 - 6x^2 + 3 \\ H_5(x) &= x^5 - 10x^3 + 15x \\ H_6(x) &= x^6 - 15x^4 + 45x^2 - 15 \end{aligned}$

と計算される．

以上を用いて， $Z = \frac{\sqrt{N}(\bar{X} - \mu)}{\sigma}$

がどれだけ速く正規分布$N(0,1)$に分布収束するかを調べることができる． $Z$の特性関数を$\phi_Z(t)$，$X$が従う分布の特性関数を$\phi(t)$とする．まず，$Z$の特性関数は

\[\phi_Z(t) = \Big\{\phi\Big(\frac{t}{\sqrt{N}\sigma}\Big)\Big\}^N\exp{\Big\{\frac{-\sqrt{N}it\mu}{\sigma}\Big\}}\]

であり，キュムラント母関数は

\[\begin{aligned} K_Z(t) &= N\log{\Big\{\phi\Big(\frac{t}{\sqrt{N}\sigma}\Big)\Big\}} - \frac{\sqrt{N}it\mu}{\sigma} \\ &= N\sum^\infty_{j=2}\Big(\frac{it}{\sigma\sqrt{N}}\Big)^j\frac{\kappa_j(X)}{j!} \\ &= \frac{t^2}{2} + \frac{(it)^3\kappa_3(X)}{6\sqrt{N}\sigma^3} + \frac{(it)^4\kappa_4(X)}{24N\sigma^4} + O(N^{-3/2}) \end{aligned}\]

と計算できる．反転定理から，

\[\begin{aligned} f_Z(z) &= \frac{1}{2\pi}\int^\infty_{-\infty}e^{-itz}\phi_Z(t)dt \\ &= \frac{1}{2\pi}\int^\infty_{-\infty}e^{-itz}\exp{\{K_Z(t)\}}dt \\ &= \frac{1}{2\pi}\int^\infty_{-\infty}e^{-itz}\exp{\Big\{\frac{t^2}{2} + \frac{(it)^3\kappa_3(X)}{6\sqrt{N}\sigma^3} + \frac{(it)^4\kappa_4(X)}{24N\sigma^4} + O(N^{-3/2})\Big\}}dt \\ &= \frac{1}{2\pi}\int^\infty_{-\infty}e^{-itx}e^{-t^2/2}\Big\{1 + \frac{(it)^3\rho_3}{6\sqrt{N}} + \frac{(it)^4\rho_4}{24N} + \frac{(it)^6\rho^2_3}{72N} + O(N^{-3/2})\Big\}dt \end{aligned}\]

ここで，$\rho_j = \kappa_j(X)/\sigma^j$は標準化されたキュムラント．これは，$c$を定数として，

\[(-1)^r\int^\infty_{-\infty}(-1)^re^{-itz}e^{-t^2/2}(it)^rc\]

の形の項の和になっていることがわかる．

\[(-1)^re^{-itz}(it)^r = \frac{d^r}{(dz)^r}e^{itz}\]

であることに注意し，積分と微分の交換を許すとすると，

\[c(-1)^r\frac{d^r}{(dz)^r}\int^\infty_{-\infty}e^{-itz}e^{-t^2/2}dt\]

と変形できる．反転定理から，

\[\begin{aligned} \int^\infty_{-\infty}e^{-itz}e^{-t^2/2}dt = \varphi(z). \end{aligned}\]

であるので，最後に$Z$から$\bar{X}$への変数変換によって

\[\begin{aligned} f_{\bar{X}}(\bar{x}) &= \frac{\sqrt{N}}{\sigma}\varphi(z)\Big\{1 + \frac{\rho_3}{6\sqrt{N}}H_3(z) + \frac{\rho_4}{24N}H_4(z) + \frac{\rho^2_3}{72N}H_6(z) + O(N^{-3/2})\Big\} \end{aligned}\]

が得られる．ここで$z=\frac{\sqrt{N}(\bar{x}-\mu)}{\sigma}$かつ，$\varphi(z)$は標準正規分布の密度関数．

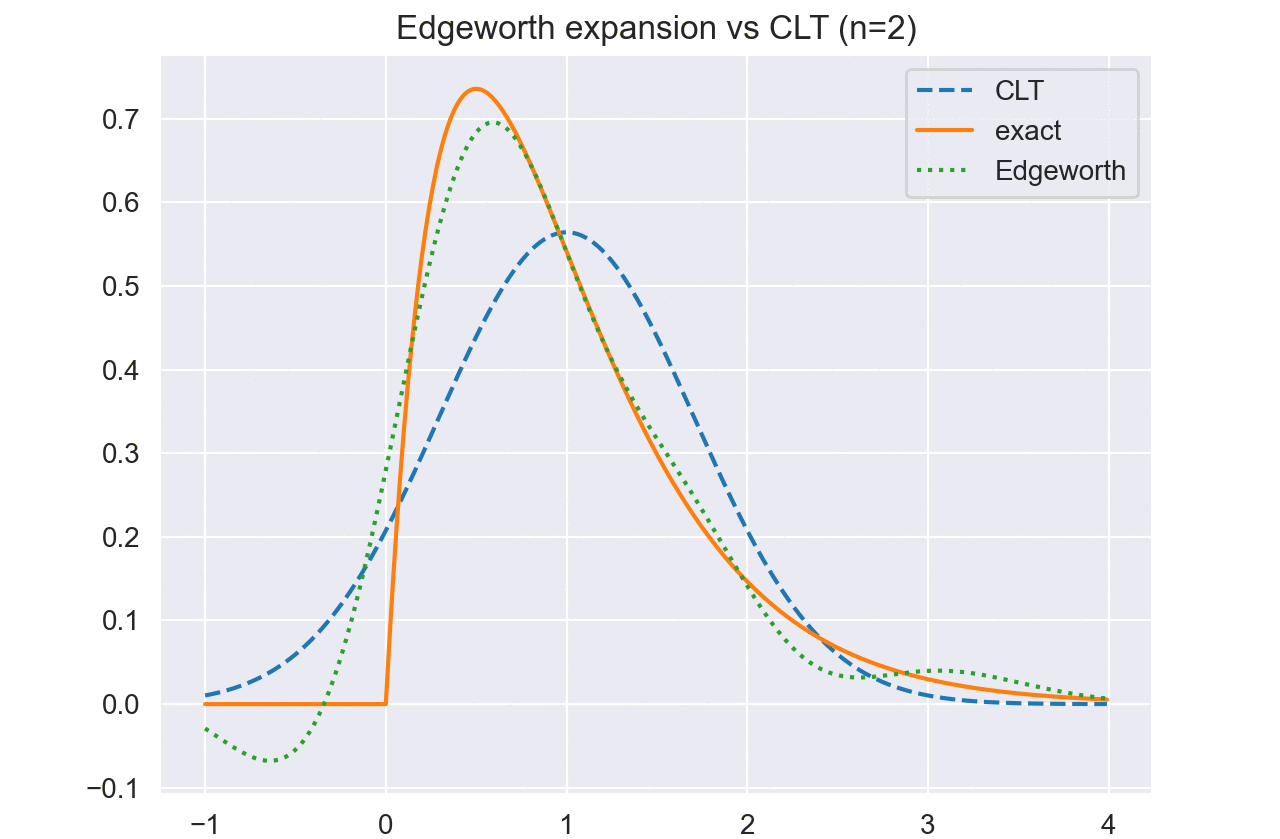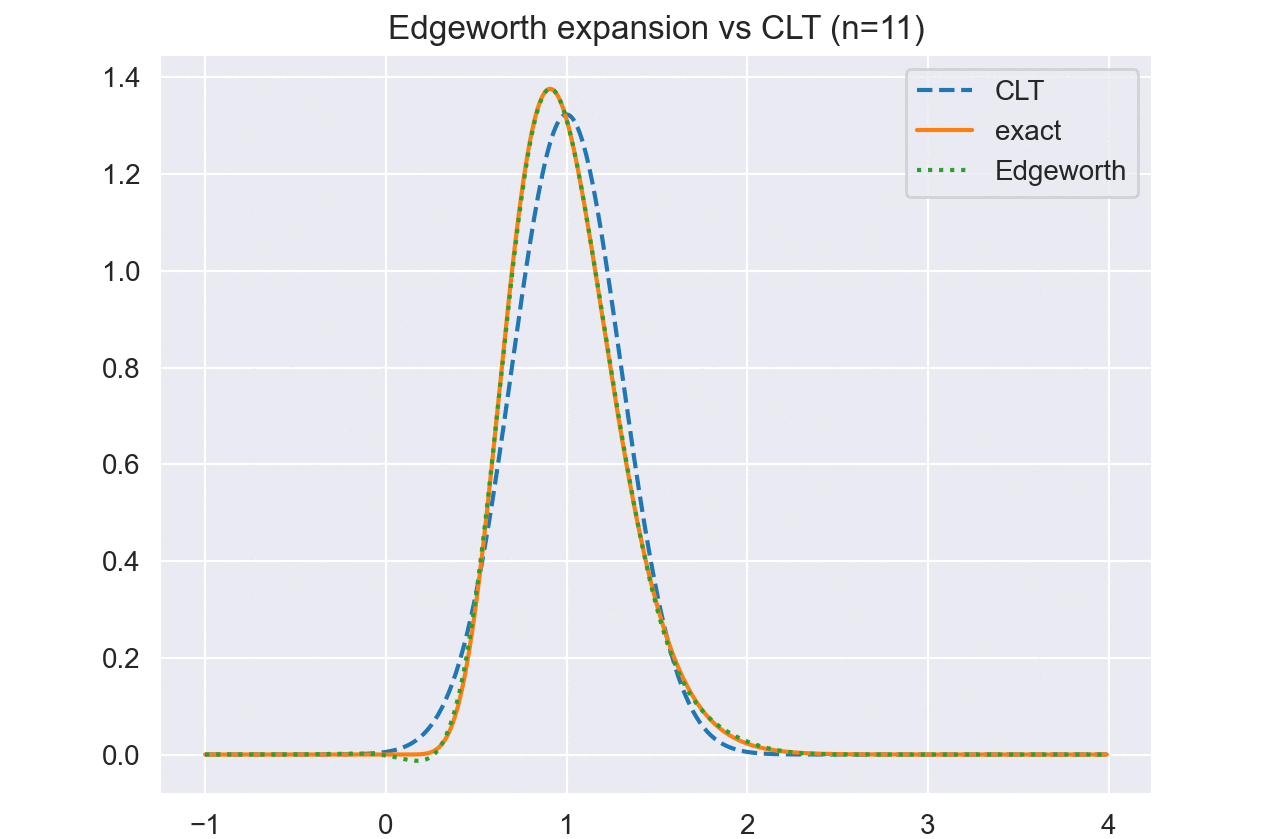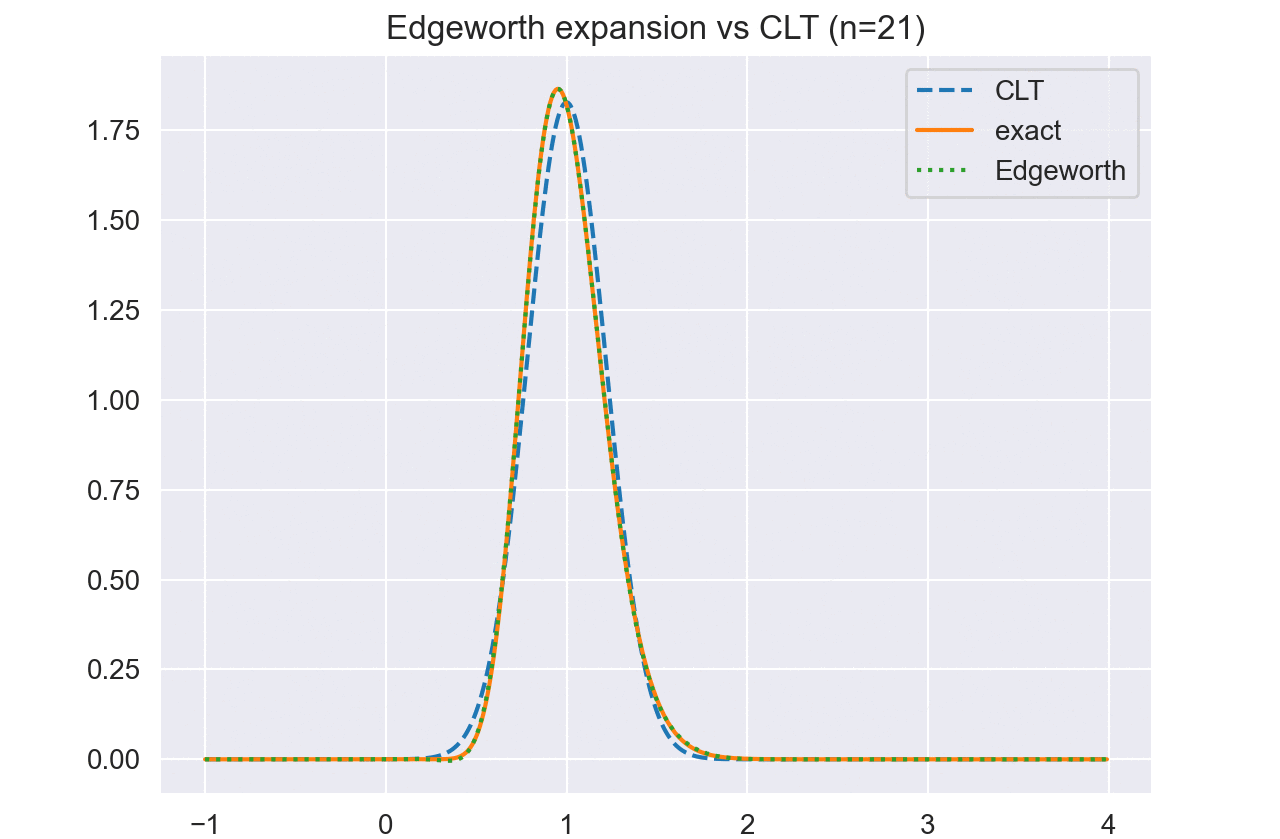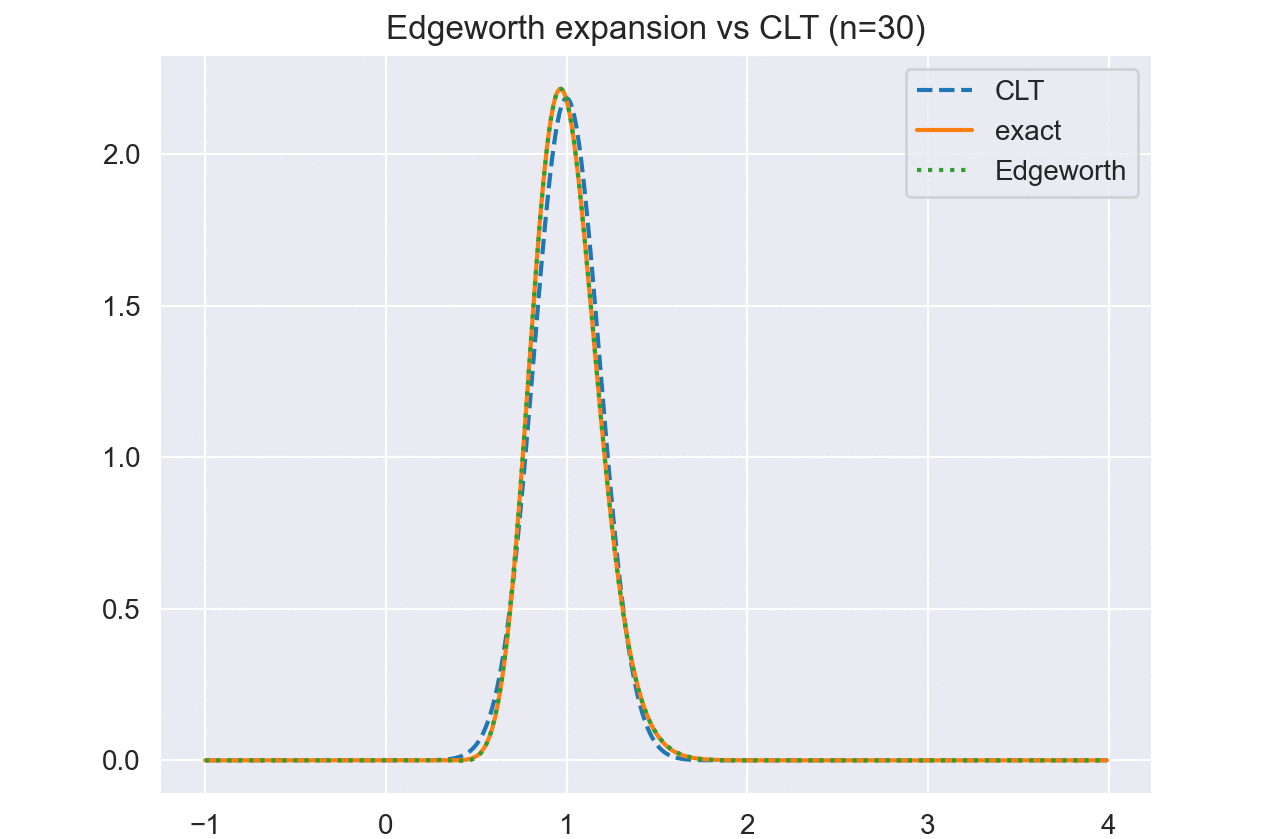
例 5. $N$個の独立な観測が$X_i\sim Exp(\lambda)$として生成されているとする．指数分布のキュムラントは

\[\kappa_j = \lambda^j(j-1)!\]

と計算できる．また，積率母関数を評価すると，和の従う分布は$\sum X_i\sim Gamma(N,\lambda)$であり，標本平均は$\bar{X}\sim Gamma(N, \lambda/N)$となることがわかる．

従って，$\bar{X}$のEdgeworth展開は

\[\begin{aligned} \rho_j &= \frac{\kappa_j(X)}{\sigma^j} = \frac{\lambda^j(j-1)!}{\lambda^j} = (j-1)! \\ f_{\bar{X}}(\bar{x}) &= \frac{\sqrt{N}}{\lambda}\varphi(z)\Big\{1 + \frac{2!}{6\sqrt{N}}(z^3-3z) + \frac{3!}{24N}(z^4-6z^2+3) \\ &\ + \frac{(2!)^2}{72N}(z^6 - 15z^4 + 45z^2 - 15) + O(n^{-3/2})\Big\} \end{aligned}\]

$N=5$での指数分布の標本平均の分布．中心極限定理による近似，Edgeworth展開による近似および真の分布をプロット．